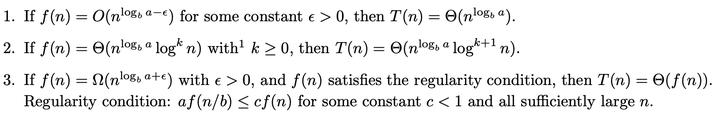MIT6.046算法设计 R1 矩阵乘法与主定理 学习笔记

带权区间调度

在L1中我们学习了区间调度

现在对每个任务加权,要如何处理得到最大和?

假设每一个任务都是潜在的第一个被执行的任务,将这个任务设为任务j,则得到他的权重w[j];

对于j后面的任务,我们也进行同样的尝试,定义Rj为{ i | s(i) > f(j)},解释一下,Rj是请求的集合,其中他们的完成时间晚于第j个请求的停止时间

我们称原来的问题为WIS(1,2,….n),则可以将其拆分为若干子问题

WIS: Weighted Interval Scheduling 带权区间调度

最终不断地解决子问题,最后得到答案为 max(j<=j<=n){w[j]+WIS(R[j])}, 时间复杂度为n^2

Can we do better?

哪里拖慢了效率?

上面的方法对所有的子问题都进行了尝试,包括那些明显不满足条件的

image-20231014114846004

具体来说,当我们尝试了请求2作为开始的请求后,对于以请求3开始的子问题,其实是请求2作为开头的请求的子问题,就是 以请求3开头的结果的权重和 等于 以2开头的权重和 减去 请求2的权重

而上面的算法又从头对以2开头的子问题 的 子问题进行了一次计算,造成了重复计算, 明明只需要减去2的权重就完事了,不是吗

Let’s do this

对上面的算法进行改造,根据分析,显然不应该尝试所有可能的请求

问题来了,如何找到适合作为开头的请求?

对于上面图中的例子,显然只选择1,2是更好的

将请求按照开始时间进行排序,我们应该首先考虑开始时间较早的请求

考虑一个问题: 如何取舍请求1呢

WIS(1,2…,n)= max{WIS(2,…,n)+w[1],WIS(R1)}

解释: 在考虑请求1的权值和 与 在请求1结束后开始的所有可能结果进行比较

递归树图

image-20231014120541132

开始解决问题
  1. 对所有请求,按照开始时间进行递增排序 O(nlogn)
  2. 参考上图的递归树,进行自底向上递归 O(n)

复杂度为O(nlogn)

小结

改进后的算法,对于每个子问题,只需要进行一次max计算(因为子问题已经在自底向上的过程中被算过了,只需要加一次当前判断的权; )

而对于改进前的的算法,每一层向上递归都会增加一个可能性,而且需要进行重复计算,所以他的层数是1+2+3+…+n,复杂度为O(n^2)

矩阵乘法中的Strassen算法

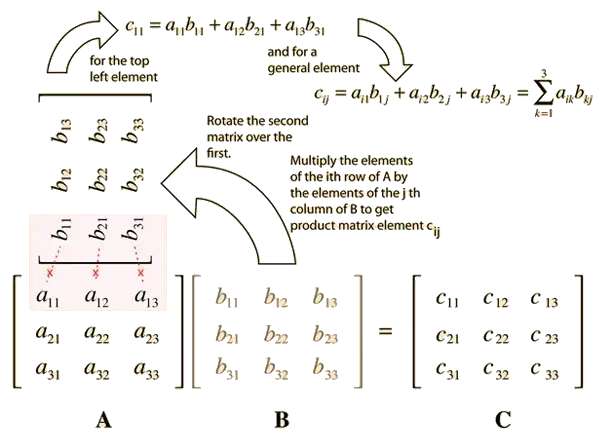
矩阵乘法, 很复杂吧?

img

显然,这个朴素的算矩阵乘法的时间复杂度为O(n^3)

我超,Strassen!

没想到吧,存在小于O(n^3)的算法

image-20231014122607096

得到递推公式

T(n) = 8*T(n/2) + O((n/2)^2) (8次矩阵乘法,4次矩阵加法 + 矩阵合并)

Strassen实现步骤

  1. 按上述方法将ABC分解 O(n)

  2. 创建如下矩阵 O(n^2)
    image-20231014124011533

  3. 递归计算如下7个矩阵
    image-20231014124034863

  4. 通过P计算C O(n^2)
    image-20231014124115289

以上步骤来自:
详解矩阵乘法中的Strassen算法 - Coder LL的文章 - 知乎 https://zhuanlan.zhihu.com/p/78657463

Master Theorem 主定理

主定理是用来

求解递如下归算法的时间复杂度..

T(n) = aT(n/b) + f(n)

有三种情况

img

image-20231014130322858

参考:
主定理(Master Theorem) - John Liu的文章 - 知乎 https://zhuanlan.zhihu.com/p/113406812