题目:AcWing 4738.快乐子数组

我们将 F(B,L,R) 定义为整数数组 B 的索引从 L 到 R（包括两者）的子数组的各个元素之和。

更具体的说，F(B,L,R)=BL+BL+1+…+BR。

如果一个长度为 K 的整数数组 C 满足其所有前缀和均为非负整数，则称数组 C 为快乐数组。

更具体的说，如果 F(C,1,1),F(C,1,2),…,F(C,1,K) 均为非负整数，则数组 C 为快乐数组。

给定一个包含 N 个整数的数组 A，请你计算数组 A 中的所有快乐连续子数组的元素和相加的结果。

大佬代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//菜,自己润不出来
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
long long p[N], pp[N], r[N];
//设p数组的前缀和数组为pp, pp[i]=p[1]+p[2]+…+p[i]
//定义r[l]为， 以al开始的最长快乐子数组的右端点。

int main () {
    int T; cin >> T;
    
    for (int t = 1; t <= T; t ++)
    {
        int n; cin >> n;
        for (int i = 1; i <= n; i ++)
        {
            int x; scanf("%d", &x);
            p[i] = p[i - 1] + x;
            pp[i] = pp[i - 1] + p[i];
        }

        stack<int> stk;
        stk.push(n + 1), p[n + 1] = -1e9;//初始化栈
        for (int i = n; i >= 0; i --) 
        {
            while (p[i] <= p[stk.top()])//当栈顶元素大时
                stk.pop();//直接删除栈顶元素
                
            r[i + 1] = stk.top();//找到了右端点
            stk.push(i);
        }

        long long res = 0;
        for (int i = 1; i <= n; i ++) {
            int j = r[i] - 1;
            res += pp[j] - pp[i - 1] - (j - i + 1) * p[i - 1];
        }
        cout << "Case #" << t << ": " << res << endl;
    }
    return 0;
}

再贴一个单调栈的文章吧

单调栈

算法原理:
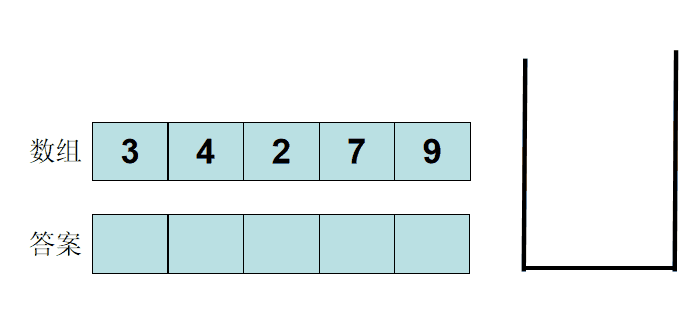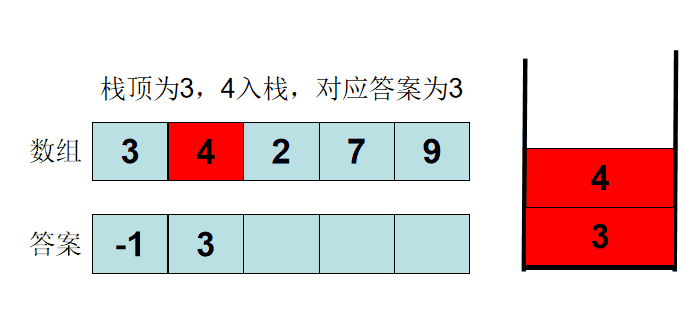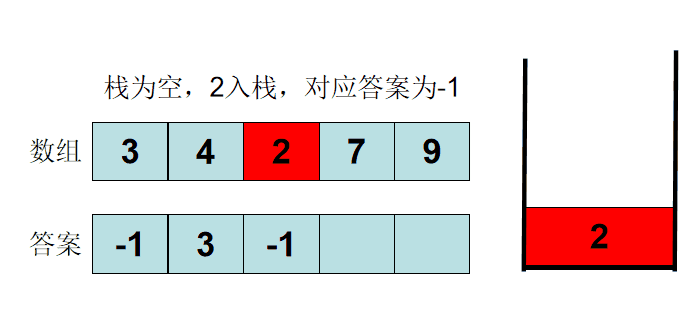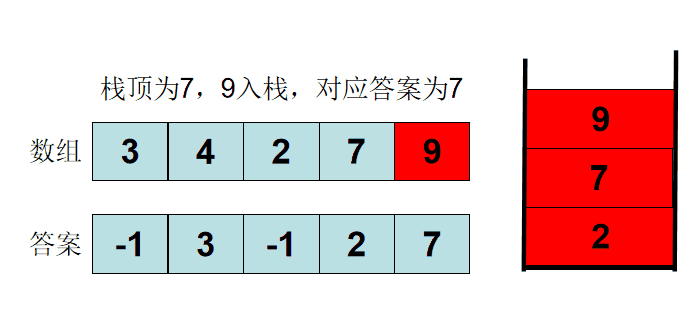
用单调递增栈，当该元素可以入栈的时候，栈顶元素就是它左侧第一个比它小的元素。
以：3 4 2 7 5 为例，过程如下：
image

这里是伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
stack<int> st;
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{
	if (栈空 || 栈顶元素大于等于当前比较元素)
	{
		入栈;
	}
	else
	{
		while (栈不为空 && 栈顶元素小于当前元素)
		{
			栈顶元素出栈;
			更新结果;
		}
		当前数据入栈;
	}
}
————————————————
版权声明：本文为CSDN博主「lucky52529」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/lucky52529/article/details/89155694

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
using namespace std;
const int N = 100010;
int stk[N], tt;

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        while (tt && stk[tt] >= x) tt -- ;//如果栈顶元素大于当前待入栈元素，则出栈
        if (!tt) printf("-1 ");//如果栈空，则没有比该元素小的值。
        else printf("%d ", stk[tt]);//栈顶元素就是左侧第一个比它小的元素。
        stk[ ++ tt] = x;
    }
    return 0;
}